Can We Use Mixture Models to Predict Market Bottoms? (Part 2)
/Post Outline
- Recap
- Model Update
- Model Testing
- Model Results
- Conclusions
- Code
Recap
In the previous post I gave a basic "proof" of concept, where we designed a trading strategy using Sklearn's implementation of Gaussian mixture models. The strategy attempts to predict an asset's return distribution such that returns that fall outside the predicted distribution are considered outliers and likely to mean revert. It showed some promise but had many areas in need of improvement.
Model Update
In this version I've refactored a lot of the code into a more object oriented structure. Now the code uses three classes.
- ModelRunner() class - This is the class for executing the model and returning our prediction dataframe and some key parameters.
- ResultEval() class - This takes the data from the prediction dataframe and key parameters and outputs our strategy returns and summary information.
- ModelPlots() class - This takes our data and outputs key plots to help visualize the strategy performance.
I did this for several reasons.
- Reduce the likelihood of input errors by creating objects that share parameters.
- Increase the ease of model testing.
- Increase interpretability.
Model Testing
In this version, we are going to expand the analysis to include other, actively traded ETFs, and test the reproducibility of the results, and generalization ability of the model.
Here are the ETFs we will examine:
symbols = ['SPY', 'DIA', 'QQQ', 'GLD', 'TLT', 'EEM', 'ACWI']
Assuming the correct imports, with the refactored code we can run the model in the following fashion. We'll focus on the TOO_LOW events although I encourage readers to experiment with both.
# Project Directory
DIR = 'YOUR/PROJECT/DIRECTORY/'
# get fed data
f1 = 'TEDRATE' # ted spread
f2 = 'T10Y2Y' # constant maturity ten yer - 2 year
f3 = 'T10Y3M' # constant maturity 10yr - 3m
factors = [f1, f2, f3]
ft_cols = factors + ['lret']
start = pd.to_datetime('2002-01-01')
end = pd.to_datetime('2017-01-01')
symbols = ['SPY', 'DIA', 'QQQ', 'GLD', 'TLT', 'EEM', 'ACWI']
for mkt in symbols:
data = get_mkt_data(mkt, start, end, factors)
# Model Params
# ------------
a, b = (.2, .7) # found via coarse parameter search
alpha = 0.99
max_iter = 100
k = 2 # n_components
init = 'random' # or 'kmeans'
nSamples = 2_000
year = 2009 # cutoff
lookback = 1 # years
step_fwd = 5 # days
MR = ModelRunner(data, ft_cols, k, init, max_iter)
dct = MR.prediction_cycle(year, alpha, a, b, nSamples)
res = ResultEval(dct, step_fwd=step_fwd)
event_dict = res._get_event_states()
event = list(event_dict.keys())[1] # TOO_LOW
post_events = res.get_post_events(event_dict[event])
end_vals = res.get_end_vals(post_events)
smry = res.create_summary(end_vals)
p()
p('*'*25)
p(mkt, event.upper())
p(smry.T)
mp = ModelPlots(mkt, post_events, event, DIR, year)
mp.plot_pred_results(dct['pred'], dct['year'], dct['a'], dct['b'])
mp.plot_equity_timeline()
In this post I'm going to skip to the results and conclusions, and provide the refactored code at the end.
Model Results
First let's look at the model results using SPY.
The first thing I noticed was that the confidence intervals were less responsive to increases in return volatility. The difference shows up in the reduction in accuracy. In Part 1, I believe the accuracy was ~71% whereas in the updated model the accuracy has dipped to ~68%! Does that hurt our strategy?
Judging by the equity curve, our strategy is not noticeably impacted by the reduced model accuracy!
The plotted equity curve is the cumulative sum of each event's returns assuming every event was a "trade". This should include overlapping events.
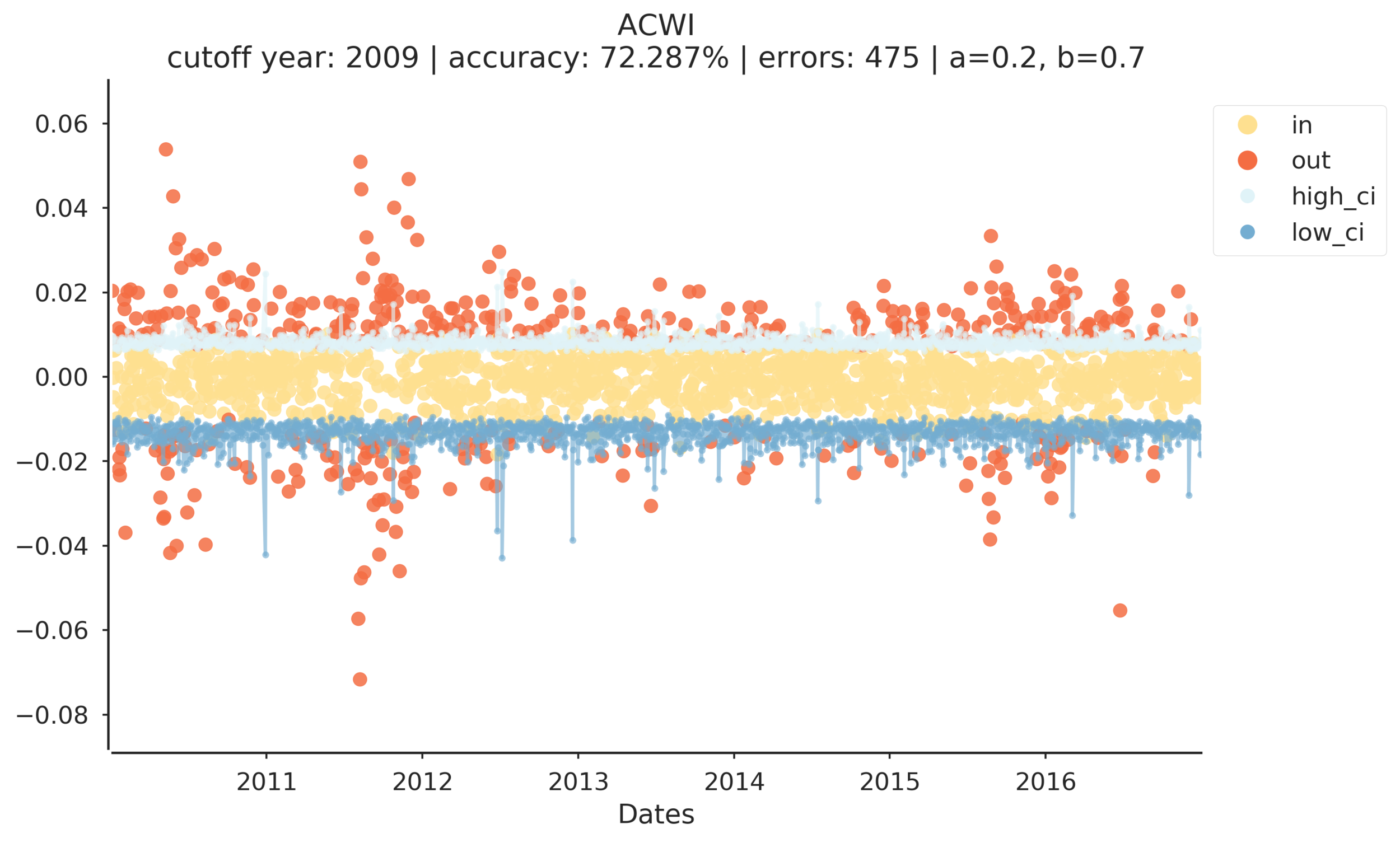
Let's look at the model results for the other ETFs.
The model has some interesting output. Notice that model accuracy ranges from ~57% (TLT) to ~83% (EEM). However, both of these equity curves end positively. GLD is distinctly volatile, and ends poorly, however the model was 75% accurate. DIA, QQQ, SPY, and ACWI all have stable sharply positive equity curves.
Conclusions
This supports my initial findings that model accuracy seems loosely, if at all, related to the strategy's equity curve. These results do indicate that the strategy is worth further evaluation but I'm hesitant to declare success.
I need to test the strategy over a longer period of time and make sure to include 2008/9. Also, I need to drill down into evaluating the strategy results vs the correlation of asset returns. For example, DIA, QQQ, and SPY are highly correlated, so we would expect the strategy to have similar results among those ETFs, but what about negatively and uncorrelated assets? TLT is generally negatively correlated with SPY while GLD is likely uncorrelated. Is the strategy performance for those two ETFs representative of other negatively/uncorrelated ETFs?
Code
%load_ext watermark
%watermark
import pandas as pd
import pandas_datareader.data as web
import numpy as np
import sklearn.mixture as mix
import scipy.stats as scs
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import missingno as msno
from tqdm import tqdm
import warnings
warnings.filterwarnings("ignore")
import affirm
sns.set(font_scale=1.25)
style_kwds = {'xtick.major.size': 3, 'ytick.major.size': 3,
'font.family':u'courier prime code', 'legend.frameon': True}
sns.set_style('white', style_kwds)
p=print
p()
%watermark -p pandas,pandas_datareader,numpy,scipy,sklearn,matplotlib,seaborn
# **********************************************************************
def get_mkt_data(mkt, start, end, factors):
"""Function to get benchmark data from
Yahoo and Factor data from FRED
Params:
mkt : str(), symbol
start : pd.DateTime()
end : pd.DateTime()
factors : list() of str()
Returns:
data : pd.DataFrame()
"""
MKT = (web.DataReader([mkt], 'yahoo', start, end)['Adj Close']
.rename(columns={mkt:mkt})
.assign(lret=lambda x: np.log(x[mkt]/x[mkt].shift(1)))
.dropna())
data = (web.DataReader(factors, 'fred', start, end)
.join(MKT, how='inner')
.dropna())
return data
# **********************************************************************
class ModelRunner():
def __init__(self, *args, **kwargs):
"""Class to run mixture model model
Params:
data : pd.DataFrame()
ft_cols : list() of feature columns str()
k : int(), n_components
max_iter : int(), max iterations
init : str() {random, kmeans}
"""
self.data = data
self.ft_cols = ft_cols
self.k = k
self.max_iter = max_iter
self.init = init
np.random.seed(123457) # make results reproducible
def _run_model(self, bgm=None, **kwargs):
"""Function to run mixture model
Params:
data : pd.DataFrame()
ft_cols : list of str()
k : int(), n_components
max_iter : int()
init : str() {random, kmeans}
Returns:
model : sklearn model object
hidden_states : array-like, hidden states
"""
X = self.data[self.ft_cols].values
if bgm:
model = mix.BayesianGaussianMixture(n_components=self.k,
max_iter=self.max_iter,
init_params=self.init,
**kwargs,
).fit(X)
else:
model = mix.GaussianMixture(n_components=self.k,
max_iter=self.max_iter,
init_params=self.init,
**kwargs,
).fit(X)
hidden_states = model.predict(X)
return model, hidden_states
def _get_state_est(self, model, hidden_states):
"""Function to return estimated state mean and state variance
Params:
model : sklearn model object
hidden_states : {array-like}
Returns:
mr_i : mean return of last estimated state
mvar_i : model variance of last estimated state
"""
# get last state
last_state = hidden_states[-1]
# last value is mean return for ith state
mr_i = model.means_[last_state][-1]
mvar_i = np.diag(model.covariances_[last_state])[-1]
return mr_i, mvar_i
def _get_ci(self, mr_i, mvar_i, alpha, a, b, nSamples):
"""Function to sample confidence intervals
from the JohnsonSU distribution
Params:
mr_i : float()
mvar_i : float()
alpha : float()
a : float()
b : float()
nsamples : int()
Returns:
ci : tuple(float(), float()), (low_ci, high_ci)
"""
rvs_ = scs.johnsonsu.rvs(a, b, loc=mr_i, scale=mvar_i, size=nSamples)
ci = scs.johnsonsu.interval(alpha=alpha, a=a, b=b,
loc=np.mean(rvs_), scale=np.std(rvs_))
return ci
def prediction_cycle(self, *args, **kwargs):
"""Function to make walk forward predictions from cutoff year onwards
Params:
year : int(), cutoff year
alpha : float()
a : float()
b : float()
nsamples : int()
Returns:
dict() :
pred : pd.DataFrame()
year : str()
a, b : float(), float()
"""
cutoff = year
train_df = self.data.ix[str(cutoff - lookback):str(cutoff)].dropna()
oos = self.data.ix[str(cutoff+1):].dropna()
# confirm that train_df end index is different than oos start index
assert train_df.index[-1] != oos.index[0]
# create pred list to hold tuple rows
preds = []
for t in tqdm(oos.index):
if t == oos.index[0]:
insample = train_df
# run model func to return model object and hidden states using params
model, hstates = self._run_model(**kwargs)
# get hidden state mean and variance
mr_i, mvar_i = self._get_state_est(model, hstates)
# get confidence intervals from sampled distribution
low_ci, high_ci = self._get_ci(mr_i, mvar_i, alpha, a, b, nSamples)
# append tuple row to pred list
preds.append((t, hstates[-1], mr_i, mvar_i, low_ci, high_ci))
# increment insample dataframe
insample = data.ix[:t]
cols = ['ith_state', 'ith_ret', 'ith_var', 'low_ci', 'high_ci']
pred = (pd.DataFrame(preds, columns=['Dates']+cols)
.set_index('Dates').assign(tgt = oos['lret']))
# logic to see if error exceeds neg or pos CI
pred_copy = pred.copy().reset_index()
# Identify indices where target return falls between CI
win = pred_copy.query("low_ci < tgt < high_ci").index
# create list of binary variables representing in/out CI
in_rng_list = [1 if i in win else 0 for i in pred_copy.index]
# assign binary variables sequence to new column
pred['in_rng'] = in_rng_list
return {'pred':pred, 'year':year, 'a':a, 'b':b}
# **********************************************************************
class ResultEval():
def __init__(self, data, step_fwd):
"""Class to evaluate prediction results
Params:
data : dict() containing results of ModelRunner()
step_fwd : int(), number of days to evalute post event
"""
self.df = data['pred'].copy().reset_index()
self.step_fwd=step_fwd
def _get_event_states(self):
"""Function to get event indexes
Index bjects must be called 'too_high', 'too_low'
Returns:
dict() : values are index objects
"""
too_high = self.df.query("tgt > high_ci").index
too_low = self.df.query("tgt < low_ci").index
return {'too_high':too_high, 'too_low':too_low}
def get_post_events(self, event):
"""Function to return dictionary where key, value is integer
index, and Pandas series consisting of returns post event
Params:
df : pd.DataFrame(), prediction df
event : {array-like}, index of target returns that exceed CI high or low
step_fwd : int(), how many days to include after event
Returns:
after_event : dict() w/ values = pd.Series()
"""
after_event = {}
for i in range(len(event)):
tmp_ret = self.df.ix[event[i]:event[i]+self.step_fwd, ['Dates','tgt']]
# series of returns with date index
after_event[i] = tmp_ret.set_index('Dates', drop=True).squeeze()
return after_event
def get_end_vals(self, post_events):
"""Function to sum and agg each post events' returns"""
end_vals = []
for k in post_events.keys():
tmp = post_events[k].copy()
tmp.iloc[0] = 0 # set initial return to zero
end_vals.append(tmp.sum())
return end_vals
def create_summary(self, end_vals):
"""Function to take ending values and calculate summary
Will fail if count of ending values (>0) or (<0) is less than 1
"""
gt0 = [x for x in end_vals if x>0]
lt0 = [x for x in end_vals if x<0]
assert len(gt0) > 1
assert len(lt0) > 1
summary = (pd.DataFrame(index=['value'])
.assign(mean = f'{np.mean(end_vals):.4f}')
.assign(median = f'{np.median(end_vals):.4f}')
.assign(max_ = f'{np.max(end_vals):.4f}')
.assign(min_ = f'{np.min(end_vals):.4f}')
.assign(gt0_cnt = f'{len(gt0):d}')
.assign(lt0_cnt = f'{len(lt0):d}')
.assign(sum_gt0 = f'{sum(gt0):.4f}')
.assign(sum_lt0 = f'{sum(lt0):.4f}')
.assign(sum_ratio = f'{sum(gt0) / abs(sum(lt0)):.4f}')
.assign(gt_pct = f'{len(gt0) / (len(gt0) + len(lt0)):.4f}')
.assign(lt_pct = f'{len(lt0) / (len(gt0) + len(lt0)):.4f}')
)
return summary
# **********************************************************************
class ModelPlots():
def __init__(self, mkt, post_events, event_state, project_dir, year):
"""Class to visualize prediction results and summary
Params:
mkt : str(), symbol
post_events : dict() of pd.Series()
event_state : str(), 'too_high', 'too_low'
project_dir : str()
year : int(), cutoff year
"""
self.mkt = mkt
self.post_events = post_events
self.event_state = event_state
self.DIR = project_dir
self.year = year
def plot_equity_timeline(self):
"""Function to plot event timeline with equity curve second axis"""
agg_tmp = []
fig, ax = plt.subplots(figsize=(10, 7))
ax1 = ax.twinx()
ax.axhline(y=0, color='k', lw=3)
for k in self.post_events.keys():
tmp = self.post_events[k].copy()
tmp.iloc[0] = 0 # set initial return to zero
agg_tmp.append(tmp)
if tmp.sum() > 0: color = 'dodgerblue'
else: color = 'red'
ax.plot(tmp.index, tmp.cumsum(), color=color, alpha=0.5)
ax.set_xlim(pd.to_datetime(str(self.year) + '-12-31'), tmp.index[-1])
ax.set_xlabel('Dates')
ax.set_title(f"{self.mkt} {self.event_state.upper()}", fontsize=16)
#sns.despine(offset=2)
agg_df = pd.concat(agg_tmp).cumsum()
ax1.plot(agg_df.index, agg_df.values, color='k', lw=5)
ax.set_ylabel('Event Returns')
ax1.set_ylabel('Equity Curve')
fig.savefig(self.DIR + f'{self.mkt} {self.event_state.upper()} post events timeline {pd.datetime.today()}.png', dpi=300)
return
def plot_events_timeline(self):
"""Function to plot even timeline only"""
fig, ax = plt.subplots(figsize=(10, 7))
ax.axhline(y=0, color='k', lw=3)
for k in self.post_events.keys():
tmp = self.post_events[k].copy()
tmp.iloc[0] = 0 # set initial return to zero
if tmp.sum() > 0: color = 'dodgerblue'
else: color = 'red'
ax.plot(tmp.index, tmp.cumsum(), color=color, alpha=0.5)
ax.set_xlim(pd.to_datetime('2009-12-31'), tmp.index[-1])
ax.set_xlabel('Dates')
ax.set_title(f"{self.mkt} {self.event_state.upper()}", fontsize=16, fontweight='demi')
sns.despine(offset=2)
fig.savefig(self.DIR + f'{self.mkt} {self.event_state.upper()} post events timeline.png', dpi=300)
return
def plot_events_post(self):
"""Function to plot events from zero until n days after"""
fig, ax = plt.subplots(figsize=(10, 7))
ax.axhline(y=0, color='k', lw=3)
for k in self.post_events.keys():
tmp = self.post_events[k].copy()
tmp.iloc[0] = 0 # set initial return to zero
if tmp.sum() > 0: color = 'dodgerblue'
else: color = 'red'
tmp.cumsum().reset_index(drop=True).plot(color=color, alpha=0.5, ax=ax)
ax.set_xlabel('Days')
ax.set_title(f"{self.mkt} {self.event_state.upper()}", fontsize=16, fontweight='demi')
sns.despine(offset=2)
fig.savefig(self.DIR + f'{self.mkt} {self.event_state.upper()} post events.png', dpi=300)
return
def plot_distplot(self, ending_values, summary):
"""Function to plot histogram of ending values"""
colors = sns.color_palette('RdYlBu', 4)
fig, ax = plt.subplots(figsize=(10, 7))
sns.distplot(pd.DataFrame(ending_values), bins=15, color=colors[0],
kde_kws={"color":colors[3]}, hist_kws={"color":colors[3], "alpha":0.35}, ax=ax)
ax.axvline(x=float(summary['mean'][0]), label='mean', color='dodgerblue', lw=3, ls='-.')
ax.axvline(x=float(summary['median'][0]), label='median', color='red', lw=3, ls=':')
ax.axvline(x=0, color='black', lw=1, ls='-')
ax.legend(loc='best')
sns.despine(offset=2)
ax.set_title(f"{self.mkt} {self.event_state.upper()}", fontsize=16, fontweight='demi')
fig.savefig(self.DIR + f'{self.mkt} {self.event_state.upper()} distplot.png', dpi=300)
return
def plot_pred_results(self, df, year, a, b):
"""Function to plot prediction results and confidence intervals"""
# colorblind safe palette http://colorbrewer2.org/
colors = sns.color_palette('RdYlBu', 4)
fig, ax = plt.subplots(figsize=(10, 7))
ax.scatter(df.index, df.tgt, c=[colors[1] if x==1 else colors[0] for x in df['in_rng']], alpha=0.85)
df['high_ci'].plot(ax=ax, alpha=0.65, marker='.', color=colors[2])
df['low_ci'].plot(ax=ax, alpha=0.65, marker='.', color=colors[3])
ax.set_xlim(df.index[0], df.index[-1])
nRight = df.query('in_rng==1').shape[0]
accuracy = nRight / df.shape[0]
ax.set_title('{:^10}\ncutoff year: {} | accuracy: {:2.3%} | errors: {} | a={}, b={}'
.format(self.mkt, year, accuracy, df.shape[0] - nRight, a, b))
in_ = mpl.lines.Line2D(range(1), range(1), color="white", marker='o', markersize=10, markerfacecolor=colors[1])
out_ = mpl.lines.Line2D(range(1), range(1), color="white", marker='o', markersize=10, markerfacecolor=colors[0])
hi_ci = mpl.lines.Line2D(range(1), range(1), color="white", marker='.', markersize=15, markerfacecolor=colors[2])
lo_ci = mpl.lines.Line2D(range(1), range(1), color="white", marker='.', markersize=15, markerfacecolor=colors[3])
leg = ax.legend([in_, out_, hi_ci, lo_ci],["in", "out", 'high_ci', 'low_ci'],
loc = "center left", bbox_to_anchor = (1, 0.85), numpoints = 1)
sns.despine(offset=2)
file_str = self.DIR+f'{self.mkt} prediction success {pd.datetime.today()}.png'
fig.savefig(file_str, dpi=300, bbox_inches="tight")
return